티스토리 뷰
https://www.acmicpc.net/problem/5639
이 문제를 해결하기 위해서는 이진 트리의 특징과 전위 순회 특징에 대한 이해가 있어야 해결할 수 있는 문제이다.
=> 즉, 트리의 특징을 제대로 이해했는지 확인하는 기본적인 문제이다.
먼저 이진 트리의 특징을 간단하게 생각해보자.
1. 2개의 자식 노드를 가진다.
이 특징으로 인해 실제 자료구조를 구현 시 배열, 인접 리스트, 포인터 등을 고려해볼 수 있게 된다.
또한 배열로 구현하게 된다면 Root 노드는 기본적으로 인덱스 1에 두는 방식을 사용하고 왼쪽 자식 노드는 2 * root index, 오른쪽 노드는 2 * root +1을 하게 된다.
인접 리스트는 다른 방법을 생각해보야 하는데, 이 문제는 트리 구조를 입력 값으로 주지 않기 때문에 위 방식을 사용하지 못한다.
문제에서는 살짝 응용된 부분은 이미 전위 순회된 결과 값을 주고 있다는 사실이다.
그렇다는 의미는 우리가 이미 알고 있는 트리를 만들기 위해서는 트리를 직접 만들어볼 수 도 있다는 뜻이다.
실제 해결된 방법에서는 트리를 직접 만들지는 않을 것이라 전위 순회를 가지고 트리를 파악하는 방법으로 살펴보자.
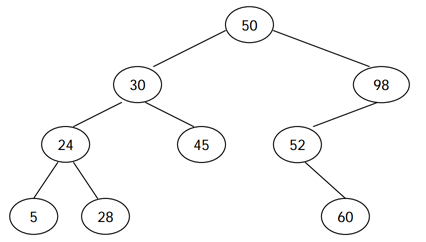
문제의 예시로 살펴본다면.. 다음과 같다.
50
30
24
5
28
45
98
52
6050, 30, 24, 5, 28, 45, 98, 52, 60
볼드 처리한 숫자를 보면 Root 50으로 부터 왼쪽, 오른쪽 자식 노드임을 알 수 있다.
왼쪽 자식 노드를 타고 내려간다면 어떨까?
30, 24, 5, 28, 45
24, 5, 28
전위 순회된 결과에서 오른쪽 자식 노드까지 탐색을 내려가는 방식으로 내려간다면 노드 탐색을 할 수 있다.
이진 트리를 만들어서 탐색을 하자가 아니라, 이진 탐색된 결과를 가지고 중위/후위 순회를 할 수 있다는 점이 이 문제의 해결 방법의 실마리다.
그렇다면 현재 서브 트리의 오른쪽 노드를 어떻게 찾을까?
순회 한번씩 하면, 나오기 때문에 간단하다.
그리고 오른쪽 자식 노드는 현재 서브트리의 Root보다 큰 값(이진 트리의 특성)임을 알 수 있다.
#include <iostream>
#include <vector>
using namespace std;
vector<int> v;
void post(int root, int end) {
if (root >= end) {
return;
}
int rightIndex = end;
for(int i = root + 1; i < end; i++) {
if(v[root] < v[i]) {
rightIndex = i;
break;
}
}
post(root + 1, rightIndex);
post(rightIndex, end);
cout << v[root] << "\n";
}
int main() {
int temp;
while (cin >> temp) {
v.push_back(temp);
}
post(0, v.size());
return 0;
}'코딩 관련 > c++' 카테고리의 다른 글
| 숨바꼭질 2 골4 (0) | 2024.11.23 |
|---|---|
| 사전 순 최대 공통 부분 수열 성공 C++ (1) | 2024.11.12 |
| 치킨 배달 C++ 골드 5 (코드 재밌어서 공유) (0) | 2024.10.16 |
| 벽 부수고 이동하기 2 (2) | 2024.09.11 |
| [프로그래머스]디스크 컨트롤러 (0) | 2024.03.20 |
